I warmly recommend Alec Radford's Theano-Tutorials to anyone interested in ML and Theano. His bare-bones approach yields remarkable clarity and effectiveness. I have adapted Alec's convolutional_net so that it works both with the MNIST dataset and on the noMNIST dataset used in the officoal tensorflow tutorial. The result is a remarkable 97.5% accuracy for the latter. To check it out you will have to build noMNIST.pickle and then place it in the data directory. Besides, comparing Theano and tensorflow may help understand each better.
Thursday, September 22, 2016
MNIST and noMNIST - Theano and tensorflow
I warmly recommend Alec Radford's Theano-Tutorials to anyone interested in ML and Theano. His bare-bones approach yields remarkable clarity and effectiveness. I have adapted Alec's convolutional_net so that it works both with the MNIST dataset and on the noMNIST dataset used in the officoal tensorflow tutorial. The result is a remarkable 97.5% accuracy for the latter. To check it out you will have to build noMNIST.pickle and then place it in the data directory. Besides, comparing Theano and tensorflow may help understand each better.
Thursday, July 14, 2016
MNIST naughties
After 500 epochs the multilayer perceptron fails on 33 of the MNIST training set images. Here are they. The y-label is their array index, while the title contains the predicted value and the (obviously different) expected value according to MNIST.

The above image is was obtained running test_3(data_set='train') from mlp_test/test_mlp.py after creating and saving the model best_model_mlp_500_zero.pkl with mlp_modified-py. Some of the expected values are truly surprising. It is hard to see how 10994 (second row, first column) can be read as a 3. The trained network identifies it, imo correctly, as a 9. The same can be said of 43454 (5th row, 5th col) and of several other images. Some ones and sevens are hard to tell apart. . I've tried training the model on a training set where the naughty images above are replaced by duplicates from the rest of training set (see load_data in mlp_modified.py to see how it's done). However, this alone does not improve performance on the test set.

Monday, June 13, 2016
Wavelet denoising
I found this interesting post about wavelet thresholding on Banco Silva's blog. Unfortunately the code does not run under PyWavelets 0.4.0/Scipy 0.17.1 , but it inspired me to write a demo which does.
One pic says more than thousand words, so here it is:
As one can see, we add so much noise that the images practically disappear, but wavelet reconstruction (db8 in this case) is smart enough to recover the main features. The key point in the code is
threshold = noiseSigma * np.sqrt(2 * np.log2(noisy_img.size)) rec_coeffs = coeffs rec_coeffs[1:] = (pywt.threshold(i, value=threshold, mode="soft") for i in rec_coeffs[1:])
Here soft thresholding is used, where the wavelet coeffiicients whose absolute value is less than the threshold are assumed to be noise and hence set to zero, so as to denoise the signal. The other coefficients are shifted by sign*theshold so as to mantain the main patterns. Here a standard Donoho-Johnstone universal threshold is used. A look at the code may tell you more.
Saturday, May 28, 2016
Minima of dml functionals
Intro
We'll have a look at the minimization of dml functionals. The code can be checked out from this github repository. It is largely based on the multilayer perceptron code from the classic deep learning theano-dml tutorial, to which some convenient functionality to initialize, save and test models has been added. The basic testing functionality is explained in readme.md.
Getting started
After checking out the repository we will first create and save the parameters of the models generated by the modified multilayer perceptron. The key parameters are set at the top of the dml/mlp_test/mlp_modified.py script.
You can modify the defaults. If you are in a hurry or have time and/or a GPU for example, you can reduce/increase the number of epochs from the default 500 to 100 or to 1000 s in the Deeplearning tutorial. We will generate two series of saved models, one where the initial values are uniformly zero (randomInit=False above) and one where the initial values of the LogRegression layer are generated randomly (randomInit=True)
First
Looking into the dml/data/models you will see files containing the parameters of the models that have been saved, one every ten epochs, as per default. Then change to randomInit=True in mlp_modified.py and repeat.
Looking at the console output or at the logs you may realise that the randomly initialised sequence has at first lower error rates than the the one initialized with zeros. However the latter catches up after a while. In my test after 500 epochs the errors are respectively 178 and 174. Don't forget to set randomInit back to False if you intend to work with SdA later.
Plotting and interpreting the results
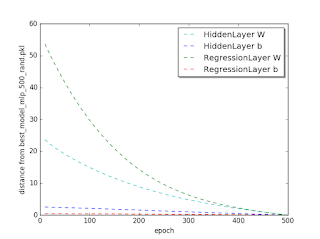
We will now see how the W and b of the HiddenLayer and of the RegressionLayer converge to their best model value, in this case the model corresponding to epoch 500. The distance that we consider is L2 norm. Using the methods in dml/mlp_test/est_compare_mlp_unit.py we get the plots.
We'll have a look at the minimization of dml functionals. The code can be checked out from this github repository. It is largely based on the multilayer perceptron code from the classic deep learning theano-dml tutorial, to which some convenient functionality to initialize, save and test models has been added. The basic testing functionality is explained in readme.md.
Getting started
After checking out the repository we will first create and save the parameters of the models generated by the modified multilayer perceptron. The key parameters are set at the top of the dml/mlp_test/mlp_modified.py script.
activation_f=T.tanh n_epochs_g=500 randomInit = False saveepochs = numpy.arange(0,n_epochs_g+1,10)
First
cd dml/mlp-test python mlp_modified.py
python mlp_modified.py
Plotting and interpreting the results
We will now see how the W and b of the HiddenLayer and of the RegressionLayer converge to their best model value, in this case the model corresponding to epoch 500. The distance that we consider is L2 norm. Using the methods in dml/mlp_test/est_compare_mlp_unit.py we get the plots.
Distance from the 500-epoch parameters for the zero initialized model
Distance from the 500-epoch parameters for the random initialized model
We see that all four parameters converge uniformly to their best value. This may correspond to our naive expectations.
Now for the most interesting bit. Do the two model series approach the same optimum? Let's have a look at the next plot.
Now for the most interesting bit. Do the two model series approach the same optimum? Let's have a look at the next plot.
Distance from the zero and the random initialized model
It is apparent that the L2 distances between the parameters are not decreasing. They two series are converging to two different optima. It is actually well known that "most local minima are equivalent and yield similar performance on a testset", but seeing it may help.
Subscribe to:
Posts (Atom)